
Lạm bàn về việc thiết kế bài toán cực trị vật lí dựa vào các bất đẳng thức phổ dụng
lượt xem 58
download
 Download
Vui lòng tải xuống để xem tài liệu đầy đủ
Download
Vui lòng tải xuống để xem tài liệu đầy đủ
Một biểu hiện cụ thể đáng kể của khoa học vật lý là khảo sát các biến cố để tìm sự tối ưu: xem xét đại lượng nào đó trong hiện tượng sao cho nó đạt đến trạng thái cực trị...
Bình luận(0) Đăng nhập để gửi bình luận!
Nội dung Text: Lạm bàn về việc thiết kế bài toán cực trị vật lí dựa vào các bất đẳng thức phổ dụng
- L M BÀN V VI C THI T K BÀI TOÁN C C TR V T LÝ D A VÀO CÁC B T ð NG TH C PH D NG. I. D N NH P : Cu c s ng là chu i quá trình ti n hoá và ñào th i. Hoà nh p vào cu c s ng, con ngư i luôn mong mu n nh ng s vi c, hi n tư ng x y ra xung quanh ta ñ t ñ n s t i ưu (optimum),viên mãn; c g ng lo i tr ñi nh ng tr ng i, kìm hãm bư c phát tri n theo quy lu t t nhiên. Nh n th c ñúng ñ n v khoa h c v t lý nói riêng và khoa h c t nhiên nói chung, thi n nghĩ v n không n m ngoài quy lu t nêu trên. M t bi u hi n c th ñáng k c a khoa h c v t lý là kh o sát các bi n c ñ tìm s t i ưu : xem xét ñ i lư ng nào ñó trong hi n tư ng sao cho nó ñ t ñ n tr ng thái c c tr (maximum and minimum). Xu t phát t ý tư ng này, chúng tôi c g ng th ñưa ra vài m u xây d ng bài toán c c tr v t lý l y ch t li u chính t các b t ñ ng th c toán h c thư ng dùng. II. CƠ S THI T K : 1. B t ñ ng th c Cauchy : (không m r ng) Thi t l p năm 1821. ði u ki n : Cho a, b ≥ 0 a+b N i dung : ≥ ab (Di n ý : Trung bình c ng 2 s không âm s ch ng 2 bao gi thua trung bình nhân c a chúng). H qu : D u “=” x y ra khi a = b. 2. B t ñ ng th c Savart : (không m r ng) ði u ki n : Cho a, b, x, y b t kỳ N i dung : ax+by ≤ (a 2 + b2 )( x 2 + y 2 ) H qu : D u “=” x y ra khi x = y = 0 ho c ay = bx (x, y không ñ ng th i tri t tiêu). 3. B t ñ ng th c Bunhiacovxki : (không m r ng) ði u ki n : Cho a, b, x, y b t kỳ N i dung : (ax+by)2 ≤ (a 2 + b 2 )( x 2 + y 2 ) H qu : D u “=” x y ra khi x = y = 0 ho c ay = bx. H qu khác : N u a = b = 1 → ( x + y )2 ≤ 2( x 2 + y 2 ) . [C n nói thêm : Thư ng nh m Bunhiacovxki là d n xu t c a Savart b ng cách bình phương 2 v . Thi t ra, Bunhiacovxki công b vào năm 1859, trong khi Savart s d ng b t ñ ng th c trong các công trình c a ông mãi t n năm
- 1884 !. Có th : tư tư ng l n thư ng g p nhau chăng ? (Nh n ñ nh c a k vi t bài này)] 4. B t ñ ng th c Bernoulli : ði u ki n : Cho a > -1 và n ∈ N* N i dung : (1 + a) n ≥ 1 + na H qu : D u “=” x y ra khi a = 0 ho c n = 1. III. PH N TRƯNG D N : 1. Dùng b t ñ ng th c Cauchy : ð tv nñ : Có n ñi n tr khác nhau : R1, R2, ……, Rn. N u m c chúng n i ti p thì ñi n tr tương ñương là Rtñ. N u m c chúng song song m i nhánh m t Rtd ñi n tr thì ñi n tr tương ñương là R’tñ. Ch ng minh r ng : ' ≥ n2 . Rtd Trư ng h p nào x y ra d u “=” ? Tìm hi u : Ta có : Rtñ = R1 + R2 + ……. + Rn V n d ng bñt Cauchy cho n s không âm : R1 + R2 + ……. + Rn ≥ n n R1R2 .............Rn (1) 1 1 1 1 Ta có : = + + ........ + R 'td R1 R2 Rn V n d ng bñt Cauchy cho n s không âm : 1 1 1 1 1 1 + + ........ ≥ n n .......... R1 R2 Rn R1 R2 Rn (2) 1 1 1 1 ⇔ + + ...... + ≥n R1 R2 Rn n R R .........R 1 2 n Rtd L y (1) x (2) v theo v ta ñư c : ' ≥ n 2 (ñpcm) Rtd D u “=” x y ra khi n ñi n tr có tr s b ng nhau. 2. Dùng b t ñ ng th c Bunhiacovxki : ð tv nñ : Dùng dây kéo v t có kh i lư ng m trư t ñ u trên m t ngang. Dây nghiêng góc α lên trên so v i phương ngang. H s ma sát trư t là µ. Ph i kéo l c F ít nh t bao nhiêu ? Lúc ñó, c n nghiêng góc α m y ñ ? Th s li u : m = 50 (kg), µ = 0,5, g = 10 (m/s2). F α m
- Tìm hi u : Phân tích l c tác d ng vào v t, vi t bi u th c ñ nh lu t II Newton, chi u bi u th c lên 2 phương Ox, Oy phù h p và t ñó tìm ñư c : m(a + µ g ) F= cosα + µ sinα Th y r ng : Fmin → (cosα + µsinα)max V n d ng bñt Bunhiacovxki : cosα + µ sinα ≤ 1+µ 2 ⇒ (cosα + µsinα ) max = 1 + µ 2 Do ñó : m( a + µ g ) 50(0 + 0,5.10) Fmin = = = 100 5 ≃ 223, 6 (N) 1+ µ 2 1 + 0, 25 M t khác, d u “=” x y ra khi sinα = µcosα → µ = tgα → α = arctg µ = arctg 0,5 ≃ 26033’ 3. Dùng b t ñ ng th c Bernoulli : ð tv nñ : Xác ñ nh l c hút m nh nh t c a trái ñ t ñ i v i tàu vũ tr “Phương ðông” ñang ñ cao h ? Th s li u : m = 2 (t n), h = 320 (km), l y g0 = 10 (m/s2), R = 6400 (km). h R O Tìm hi u : Thi t l p các bi u th c g0, gh r i suy ra : g0 mg 0 gh = 2 ⇒ Ph = mg h = 2 h h 1 + 1 + R R 2 Ta có : (Ph)max n u 1 + h R min
- V n d ng bñt Bernoulli : 2 2 h h h h 1 + ≥ 1 + 2 ⇒ 1 + = 1 + 2 R R R min R mg 0 103.10 10 Do ñó : ( Ph )max = = = .10 4 ≃ 9, 09 (kN) h 320 11 1+ 2 1+ 2 R 6400 IV. L I B T : Chúng tôi r t mong nh n ñư c nh ng ch thi u sót trong chuyên ñ này ñ rút kinh nghi m và cũng r t mong nh ng m u thi t k m i “ñ p” hơn t các th y trong t V t lý - K thu t. T V t lý-K thu t Trư ng THPT Tôn ð c Th ng.

CÓ THỂ BẠN MUỐN DOWNLOAD
-

Sáng kiến kinh nghiệm: Làm thế nào để vận dụng và thiết kế trò chơi học tập tiếng Việt lớp 5 đạt hiệu quả cao
 21 p |
21 p |  322
|
322
|  48
48
-

Câu hỏi trắc nghiệm tổng hợp môn Lập trình web
 36 p |
36 p |  555
|
555
|  43
43
-

Giáo dục kỹ năng sống mầm non: Làm thế nào để hướng dẫn trẻ thiết lập mục tiêu
 4 p |
4 p |  166
|
166
|  20
20
-

Hướng dẫn học PTS CS5 từ căn bản
 15 p |
15 p |  125
|
125
|  20
20
-

Sáng kiến kinh nghiệm: Ứng dụng công nghệ thông tin thiết kế diễn biến các chiến dịch lớn trong chương trình lịch sử Việt Nam lớp 12 giai đoạn 1945 – 1975
 12 p |
12 p |  93
|
93
|  16
16
-

Sáng kiến kinh nghiệm: Quy trình thiết kế tình huống dạy học hợp tác trong dạy học khái niệm toán học (Thể hiện qua dạy hình học lớp 10)
 23 p |
23 p |  81
|
81
|  11
11
-

Sáng kiến kinh nghiệm Mầm non: Một số biện pháp chỉ đạo nhằm tăng kỹ năng ứng dụng công nghệ thông tin trong dạy học cho giáo viên
 31 p |
31 p |  44
|
44
|  9
9
-
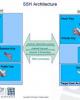
Sao lưu toàn bộ website bằng SSH Command Line
 4 p |
4 p |  82
|
82
|  7
7
-

Sáng kiến kinh nghiệm Mầm non: Ứng dụng công nghệ thông tin trong việc cho trẻ mẫu giáo 4 tuổi làm quen các biểu tượng ban đầu về toán
 13 p |
13 p |  39
|
39
|  6
6
-

Sáng kiến kinh nghiệm THPT: Phát huy tính chủ động, tích cực và sáng tạo của học sinh thông qua việc tổ chức hoạt động tự làm một số thí nghiệm đơn giản sau khi học bài Chuyển động thẳng đều (SGK Vật lí 10 THPT)
 24 p |
24 p |  36
|
36
|  5
5
-

Sáng kiến kinh nghiệm Tiểu học: Một số kinh nghiệm về thiết kế trò chơi trên phần mềm sử dụng bảng tương tác tạo hứng thú cho học sinh trong môn Toán học lớp 4
 16 p |
16 p |  65
|
65
|  5
5
-

Sáng kiến kinh nghiệm Mầm non: Một số biện pháp giúp giáo viên làm đồ chơi tự tạo cho trẻ mẫu giáo
 8 p |
8 p |  43
|
43
|  4
4
-

Sáng kiến kinh nghiệm Tiểu học: Một số giải pháp nâng cao kĩ năng giải các bài toán về sự tăng giảm tử số và mẫu số của phân số cho học sinh lớp 4 – 5
 27 p |
27 p |  81
|
81
|  4
4
-

Sáng kiến kinh nghiệm Tiểu học: Ứng dụng phần mềm Activinspire trong thiết kế bài giảng góp phần nâng cao chất lượng dạy học ở tiểu học
 9 p |
9 p |  93
|
93
|  3
3
-

Sáng kiến kinh nghiệm THPT: Thiết kế bài dạy và tổ chức các hoạt động trên lớp phần Hàm số góp phần phát triển phẩm chất, năng lực cho học sinh lớp 12
 52 p |
52 p |  62
|
62
|  3
3
-

Đề thi học kì 2 môn Công nghệ lớp 8 năm 2022-2023 có đáp án - Trường THCS Quang Dương, Đông Hưng
 4 p |
4 p |  10
|
10
|  3
3
-

Kế hoạch bài dạy Hoạt động trải nghiệm, hướng nghiệp 9: Tuần 35 (Sách Kết nối tri thức)
 16 p |
16 p |  1
|
1
|  1
1
Chịu trách nhiệm nội dung:
Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA
LIÊN HỆ
Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM
Hotline: 093 303 0098
Email: support@tailieu.vn









