
PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH MŨ VÀ LÔGARIT
lượt xem 62
download
 Download
Vui lòng tải xuống để xem tài liệu đầy đủ
Download
Vui lòng tải xuống để xem tài liệu đầy đủ
a) Phương trình mũ cơ bản có dạng: ax = m, trong đó a 0, a
Bình luận(0) Đăng nhập để gửi bình luận!
Nội dung Text: PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH MŨ VÀ LÔGARIT
- PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH MŨ VÀ LÔGARIT Dạng 1. Phương trình cơ bản a) Phương trình mũ cơ bản có dạng: a x = m , trong đó a > 0, a 1 và m là số đã cho. • Nếu m 0 , thì phương trình a x = m vô nghiệm. • Nếu m > 0 , thì phương trình a x = m có nghiệm duy nhất x = log a m . b) Phương trình lôgarit cơ bản có dạng: log a x = m , trong đó m là số đã cho. • Phương trình có điều kiện xác định là x > 0 ( a > 0, a 1 ). • Với mọi m ᄀ , phương trình log a x = m có nghiệm duy nhất x = a m . VD1. Giải các phương trình sau: 1. 5 x +1 + 6.5 x − 3.5 x −1 = 52 2. 3x +1 + 3x + 2 + 3x + 3 = 9.5x + 5x +1 + 5x + 2 3. 3x.2 x +1 = 72 2 2 2 4. 4x −3x+2 + 4x +6 x+5 = 42 x +3x+7 + 1 5. 5.32 x−1 − 7.3x−1 + 1 − 6.3x + 9x+1 VD2. Giải các phương trình sau: 1. log 3 x ( x + 2 ) = 1 2. log 2 ( x − 3) − log 2 ( 6 x − 10 ) + 1 = 0 2 3. log ( x + 15 ) + log ( 2 x − 5 ) = 2 4. log 2 ( 2 − 5 ) = x x +1 Bài tập Giải các phương trình sau: 1. 3x +1 − 2.3x − 2 = 25 2. 3.2 x +1 + 2.5 x − 2 = 5 x + 2 x − 2 2 3. 4log x +1 − 6log x = 2.3log x + 2 3 x −1 x 4 7 16 � �� � 4. � �� � − =0 7 4 49 � �� � 5. 2.5 x + 2 − 5 x +3 + 375 = 0 6. 3 2 x −5 − 5 2 x − 7 = 32 1 x +2 1 x +2 x +1 x +1 7. 2.5 − .4 − .5 = 4 5 4 8. 3 ( 10 − 6 ) + 4.10 = 5 ( 10 − 6 ) x+2 x +1 x −1 x −1 x ( x − 2 ) log 5 x = 2 log3 ( x − 2 ) 9. log 3 x −1 + log 2 ( x − 1) ( x + 4 ) = 2 10. log 2 x+4 11. log x2 16 − log x 7 = 2 4 12. 2 log 8 ( 2 x ) + log 8 ( x − 2 x + 1) = 2 3 Dạng 2. Phương pháp đưa về cùng cơ số Sử dụng công thức: α β • a =a �α =β .
- b > 0 ( ho� c > 0) c log a b = log a c • b=c VD1. Giải các phương trình sau: 1. 52 x +1 + 7 x +1 − 175 x − 35 = 0 1 x+2 1 x +1 x +1 2. 3.4 + .9 = 6.4 − .9 x 3 2 x −3 + 2 x −3 + 4 2 x +1 + 2 x −1 3. x .2 + 2 = x .2 2 4. 4 x2 + x + 21− x2 = 2( x +1) + 1 2 VD2. Giải các phương trình sau: 1. log x 2.log x 2 = log x 2 16 64 5 2. log 5 x + log5 x = 1 2 x 3. log 2 x + log 3 x + log 4 x = log 20 x 1 log 2 ( 3 x − 1) + = 2 + log 2 ( x + 1) 4. log ( x +3 ) 2 x −1 1 5. log 9 ( x 2 − 5 x + 6 ) = log 2 + log 3 x − 3 3 2 2 ( ) ( ) 2 2 6. log 2 x + 3x + 2 + log 2 x + 7 x + 12 = 3 + log 2 3 1 1 ( x + 3) + log 4 ( x − 1) = log 2 ( 4 x ) 8 log VD3. Giải phương trình sau: 2 2 4 Bài tập Giải các phương trình sau: 2 −3 x 1 x�� 1. 9 � � = 27 x 3 81x +3 3 �� 2. log 4 log 2 x + log 2 log 4 x = 2 3. 3.13x + 13x +1 − 2 x + 2 = 5.2 x +1 x −1 4. log 5 ( x 2 + 2 x − 3) = log x+3 5 5. log 4 ( x − 1) − log 4 ( x − 1) = log 4 x − 2 2 2 6. log 5 ( 6 − 4 x − x ) = 2 log 5 ( x + 4 ) 2 1 7. 2log ( x − 1) = log x5 − log x 2 ( ) 2 8. 2log9 x = log3 x.log3 2x + 1 − 1 9. log 4 ( x + 1) + 2 = log 4 − x + log8 ( 4 + x ) 2 3 2 Dạng 3. Phương pháp đặt ẩn phụ VD1. Giải các phương trình sau: 2 2 1. 4 x + x − 2 − 5.2 x −1+ x − 2 − 6 = 0 2. 43+ 2cos x − 7.41+ cos x − 2 = 0 ( 26 + 15 3 ) ( ) ( ) x x x +2 7+4 3 −2 2− 3 =1 3.
- ( 2 − 3) + ( 2 + 3) x x = 14 4. 5. 5.23 x −1 − 3.25−3 x + 7 = 0 �3 x 8 � � x 1� 6. � − 3 x � 6 � − x −1 � 1 −2 = 2 2�� 2 � � 7. 27 x + 12 x = 2.8x VD2. Giải các phương trình sau: 1. log 2 ( x + 1) = log x +1 16 ( ) x x 2. log 6.5 + 25.20 = x + log25 3. log x.log x (4 x ) = 12 2 2 2 log8 4 x log 2 x = 4. log 4 2 x log16 8 x 5. log 2 ( 4 + 4 ) .log 2 ( 4 + 1) = 3 x +1 x 6. log 4 ( log 2 x ) + log 2 ( log 4 x ) = 2 7. log x ( 125 x ) .log 25 x = 1 2 1 8. log x 3 + log 3 x = log x 3 + log 3 x + 2 4 ( 2 − log3 x ) log 9 x 3 − =1 9. 1 − log 3 x ( ) 10. log 2 x = log 3 x +2 Bài tập Giải các phương trình sau: 1. 9 x − 10.3x + 9 = 0 2 2 2. 4 x − 6.2 x + 8 = 0 2 2 2 3. 15.25 x − 34.15x + 15.9 x = 0 2 2 4. 9sin x + 9cos x = 10 ( 2 + 3) + ( 2 − 3) x x =4 5. 5 6. log 3 x + log x 3 = 2 7. 2 x log 2 x + 2 x −3log8 x − 5 = 0 8. 5 x −1 + 5.0, 2 x − 2 = 26 9. 25 x − 12.2 x − 6, 25.0,16 x = 0 1 3 10. 64 x − 23+ x + 12 = 0 11. 25log x = 5 + 4.x log5 12. 4 x − 4 x +1 = 3.2 x + x 2 2 13. 2sin x + 5.2cos x = 7 2 14. 4cos 2 x + 4cos x = 3 )( ) ( x x 4 − 15 + 4 + 15 =8 15.
- )( ) ( cos x cos x 5 7+4 3 + 7−4 3 = 16. 2 ( ) + ( 7 −3 5) x x 17. 7 + 3 5 = 14.2 x 18. 7 log25 ( 5 x ) −1 − x log5 7 = 0 2 log x 3 x .log 3 x + 1 = 0 19. log8 4 x log 2 x = 20. log 4 2 x log16 8 x 21. 1 + 2 log x + 2 5 = log 5 ( x + 2 ) 22. 5log 2 x + 2.x log2 5 = 15 23. log ( log x ) + log ( log x − 2 ) = 0 3 24. log 3 ( 3 − 1) .log ( 3 − 3) = 6 x +1 x 25. 9 x − 8.3x + 7 = 0 1 2 x −1 x −1 26. .4 + 21 = 13.4 2 1 1 1 27. 6.9 x − 13.6 x + 6.4 x = 0 28. 3 25 x − 3 9 x + 3 15x = 0 29. log 2 ( 9 − 2 ) = 3 − x x )( ) ( x x 2+ 3 + 2− 3 = 2x 30. Dạng 4. Phương pháp lôgarit VD. Giải các phương trình 4 x +1 3 x+2 2 1 �� �� 1. � � = � � 5 7 �� �� 2 2. 5 x.3x = 1 x 3. 3x.8 x + 2 = 6 Bài tập Giải các phương trình sau: 1. 4.9 x −1 = 3 22 x +1 2 −2 x .3x = 1,5 2. 2 x 2 x −1 3. 5 x.2 x +1 = 50 3x 4. 3x.2 x + 2 = 6 x x 5. 23 = 32 Dạng 5. Phương pháp sử dụng tính đồng biến và nghịch biến của hàm số VD1. Giải các phương trình: x 1. 2 x = 1 + 3 2 2. 2 3− x = − x 2 + 8 x − 14 VD2. Giải các phương trình: 1. log 2 x = 3 − x
- 2. l og 2 x + ( x − 1) log 2 x = 6 − 2 x 2 VD3. Giải các phương trình: 1. 25 − 2 ( 3 − x ) 5 + 2 x − 7 = 0 x x 2. 8 − x.2 x + 23− x − x = 0 VD4. Giải phương trình: x .3 + 3 ( 12 − 7 x ) = − x + 8 x − 19 x + 12 2x x 3 2 ( ) VD5. Giải phương trình: log 2 1 + x = log 3 x 8 22 x+1 + 23−2 x = ( ) VD6. Giải phương trình: log3 4x2 − 4x + 4 Bài tập Giải các phương trình sau: 1. ( x + 2 ) log 3 ( x + 1) + 4 ( x + 1) log 3 ( x + 1) − 16 = 0 2 2. 4 x + 9 x = 25 x 3. 3.25 + ( 3 x − 10 ) 5 + 3 − x = 0 x −2 x −2 4. 9 x + 2 ( x − 2 ) .3x + 2 x − 5 = 0 ( ) 5. x + log x − x − 6 = 4 + log ( x + 2 ) 2 ( x + 3) log3 ( x + 2 ) + 4 ( x + 2 ) log3 ( x + 2 ) = 16 2 6.

CÓ THỂ BẠN MUỐN DOWNLOAD
-

Một số bài toán giải phương trình, hệ phương trình mũ và Logarit
 10 p |
10 p |  1930
|
1930
|  489
489
-
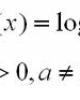
Hệ phương trình mũ và logarit
 30 p |
30 p |  1221
|
1221
|  397
397
-

Ôn tập: Hệ phương trình mũ và lôgarit
 8 p |
8 p |  566
|
566
|  148
148
-

Phương trình, bất phương trình hệ phương trình mũ và Lôgarit ( phần 2)
 74 p |
74 p |  245
|
245
|  68
68
-

Luyện thi Đại học Toán chuyên đề: Hệ phương trình mũ và Logarit - Thầy Đặng Việt Hùng
 11 p |
11 p |  295
|
295
|  58
58
-

PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH MŨ VÀ LÔGARIT
 11 p |
11 p |  274
|
274
|  39
39
-

Tuyển tập bài tập phương trình, bất phương trình, hệ phương trình, mũ, logarit
 2 p |
2 p |  196
|
196
|  36
36
-

Giáo án Giải tích 12 ban tự nhiên : Tên bài dạy : PHƯƠNG TRÌNH , HỆ PHƯƠNG TRÌNH MŨ VÀ LÔGARIT
 10 p |
10 p |  190
|
190
|  30
30
-

Toán 12: Hệ phương trình mũ và Logarit-P1 (Đáp án Bài tập tự luyện) - GV. Lê Bá Trần Phương
 4 p |
4 p |  138
|
138
|  28
28
-

PHƯƠNG TRÌNH , HỆ PHƯƠNG TRÌNH MŨ VÀ LÔGARIT
 7 p |
7 p |  248
|
248
|  25
25
-

Toán 12: Hệ phương trình mũ và Logarit-P2 (Đáp án Bài tập tự luyện) - GV. Lê Bá Trần Phương
 3 p |
3 p |  93
|
93
|  11
11
-

Luyện thi Đại học Kit 1 - Môn Toán Bài 08: Phương trình - Bất phương trình mũ và logarit
 1 p |
1 p |  98
|
98
|  8
8
-

Toán 12: Hệ phương trình mũ và Logarit-P1 (Tài liệu bài giảng) - GV. Lê Bá Trần Phương
 1 p |
1 p |  84
|
84
|  6
6
-

Toán 12: Hệ phương trình mũ và Logarit-P2 (Bài tập tự luyện) - GV. Lê Bá Trần Phương
 1 p |
1 p |  88
|
88
|  5
5
-

Toán 12: Hệ phương trình mũ và Logarit-P2 (Tài liệu bài giảng) - GV. Lê Bá Trần Phương
 1 p |
1 p |  75
|
75
|  4
4
-

Toán 12: Hệ phương trình mũ và Logarit-P1 (Bài tập tự luyện) - GV. Lê Bá Trần Phương
 1 p |
1 p |  95
|
95
|  3
3
-

Chuyên đề 3: Phương trình, bất phương trình, hệ phương trình mũ và Logarit - GV. Nguyễn Bá Trung
 11 p |
11 p |  136
|
136
|  2
2
Chịu trách nhiệm nội dung:
Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA
LIÊN HỆ
Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM
Hotline: 093 303 0098
Email: support@tailieu.vn









